t 検定の原理 #2 - 対応のある t 検定
UB3/statistics/group_comparison/t_test_pair
このページの最終更新日: 2023/02/14- 概要: 対応のある t 検定とは – どんな場合に使うのか
- 対応のある t 検定の原理
広告
概要: 対応のある t 検定とは
このページは、以下の一連の t 検定に関するページの一部である。より深く理解したい場合には、順に読むことをお勧めする。
- 仮説検定
- z 検定
- t 検定の原理 #1: 母平均の検定
- t 検定の原理 #2: 対応のある t 検定: このページ
- t 検定の原理 #3: 正規分布、等分散の場合
- Welch の t 検定: 等分散を仮定できない場合
- Mann-Whitney の U 検定: 正規分布 を仮定できない場合。ノンパラ。
- 実践 1: Excel での t 検定
対応のある t 検定は、
- 10 人が 50 m 走のタイムを測定した (データセットA)。その人たちが 1 週間のトレーニングを行い、 再び 50 m 走のタイムを計った (データセット B)。A と B のデータは同じ 10 人から得られているので対応がある。
- たとえば、10人に含まれる「鈴木さんの A のタイム」は、「鈴木さんの B のタイム」と対応している。トレーニングの効果を知りたいなら、 他の人の B のタイムではなく、鈴木さん自身の B のタイムと比較するべきである。
このページのポイントは、
広告
対応のある t 検定の原理
文献 1 の例題 4 を参考にしています。
|
例題 4 ある地区でランダムに観測点を 16 箇所 (A - P) 選び、積雪量を測定した。2 行目は昨年 1 月のデータ (cm)、3 行目は今年 1 月のデータである。 119; 117; 115; 116; 112; 121; 115; 122; 116; 118; 109; 112; 119; 112; 117; 113; 118; 115; 115; 122; 118; 121; 120; 122; 120; 113; 120; 123; 121; 121; 109; 117; この結果から、昨年 1 月と今年 1 月の積雪量の平均値は同じだと言えるか? |
まず、仮説を設定する。
帰無仮説: 積雪量の平均値は同じである。
対立仮説: 積雪量の平均値は同じでない。
となるが、ここは一工夫して以下のように差をとって表すことにする。
H0: μ1 - μ2 = 0
H1: μ1 - μ2 ≠ 0
ここで、H0 は帰無仮説、H1 は対立仮説、μ1 は昨年 1 月の積雪量の平均値、μ2 は今年 1 月の積雪量の平均値である。
次は検定統計量を求めるステップであるが、その前に、
119; 117; 115; 116; 112; 121; 115; 122; 116; 118; 109; 112; 119; 112; 117; 113;
118; 115; 115; 122; 118; 121; 120; 122; 120; 113; 120; 123; 121; 121; 109; 117;
するとこの検定は、差の値を標本集団として、
したがって、ここで用いるべき検定統計量は、m を標本平均、μ を母平均、u を標本集団の標準偏差 (不偏分散から算出)、n を標本数として
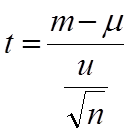
となる。
あとの手順は、t 検定の原理 - 母平均の検定と全く同じなので省略する。結果的に P = 0.058 となり、帰無仮説は棄却できない。したがって、「積雪量は同じであるとはいえない」という結論になる。
References
- MATLAB による仮説検定の基礎. Web pdf.
広告
コメント欄
サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。
